Step function
In mathematics, a function on the real numbers is called a step function (or staircase function) if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces.
Contents |
Definition and first consequences
A function 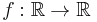 is called a step function if it can be written as
is called a step function if it can be written as
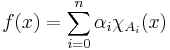 for all real numbers
for all real numbers 
where 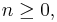
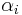 are real numbers,
are real numbers, 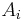 are intervals, and
are intervals, and 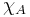 is the indicator function of
is the indicator function of  :
:
In this definition, the intervals 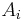 can be assumed to have the following two properties:
can be assumed to have the following two properties:
Indeed, if that is not the case to start with, a different set of intervals can be picked for which these assumptions hold. For example, the step function
can be written as
Examples
- A constant function is a trivial example of a step function. Then there is only one interval,
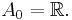
- The Heaviside function H(x) is an important step function. It is the mathematical concept behind some test signals, such as those used to determine the step response of a dynamical system.
- The rectangular function, the normalized boxcar function, is the next simplest step function, and is used to model a unit pulse.
Non-examples
- The integer part function is not a step function according to the definition of this article, since it has an infinite number of intervals. However, some authors define step functions also with an infinite number of intervals.[1]
Properties
- The sum and product of two step functions is again a step function. The product of a step function with a number is also a step function. As such, the step functions form an algebra over the real numbers.
- A step function takes only a finite number of values. If the intervals
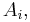
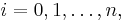 in the above definition of the step function are disjoint and their union is the real line, then
in the above definition of the step function are disjoint and their union is the real line, then 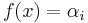 for all
for all 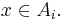
- The Lebesgue integral of a step function
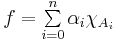 is
is 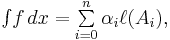 where
where 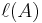 is the length of the interval
is the length of the interval 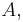 and it is assumed here that all intervals
and it is assumed here that all intervals 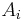 have finite length. In fact, this equality (viewed as a definition) can be the first step in constructing the Lebesgue integral.[2]
have finite length. In fact, this equality (viewed as a definition) can be the first step in constructing the Lebesgue integral.[2]
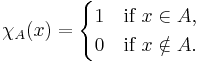
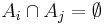 for
for 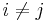
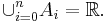
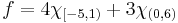
![f = 0\chi_{(-\infty, -5)} %2B4 \chi_{[-5, 0]} %2B7 \chi_{(0, 1)} %2B 3 \chi_{[1, 6)}%2B0\chi_{[6, \infty)}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/c52ea0f0793ca2c68d57711045030c4c.png)